兰伯特问题（Lambert's problem）是轨道动力学领域的经典基础性问题之一。由于在轨运行的航天器受到各种摄动的干扰，航天器的实际运行轨道会偏离经典兰伯特问题所给出的开普勒解。因此，在经典兰伯特问题中进一步考虑动力学模型中的摄动干扰，摄动兰伯特问题被提了出来以获取摄动干扰下的高精度轨道。现有摄动兰伯特问题的求解方法分为间接法和直接法。直接法是将摄动兰伯特问题转化为初始速度矢量打靶修正问题，即通过对初始速度矢量打靶修正，使得给定时间后的末端状态满足终端约束。直接法的主要挑战在于随着飞行时间的增加，终端条件对初速度的变化愈加敏感。现有基于同伦策略的改进方法改善了直接法的收敛稳定性，但计算负担大幅提升。因此，高效且稳定的摄动兰伯特问题求解器是高精度轨道计算和优化的关键，一直是航天器轨道动力学领域研究的热点。
日前，航天学院航天新技术实验室的博士研究生杨彬提出了一种新型 J2 摄动兰伯特问题快速求解器。求解器由智能初始猜测生成器和微分校正程序两部分组成。智能初始猜测生成器使用一个经过完备训练的深度神经网络预测开普勒解偏差，通过偏差修正进而得到摄动兰伯特问题的初值；微分校正模块基于上述初始猜测并采用基于前向差分的打靶算法进一步更新初始速度，获取满足精度的摄动兰伯特问题解。通过对八类不同形式样本进行相关性分析，找到了适用于J2 摄动兰伯特问题神经网络训练的最佳样本形式。所提方法通过求解木星系统中多J2摄动兰伯特问题验证了其可行性，在与经典牛顿迭代法和同伦算法的比较中，本文所提方法在计算效率和收敛稳定性上展现出突出优势。
本文考虑J2摄动干扰，提出了基于深度神经网络（Deep Neural Networks, DNN）的J2摄动兰伯特问题智能求解器，智能求解器由智能初始猜测生成模块（Intelligent initial Guess Generator, IGG）和打靶校正模块（Shooting Correction Module, SCM）组成。 IGG 中使用 DNN 来近似开普勒解的修正值，并为打靶校正模块提供初始猜测。首先，通过对笛卡尔坐标、球坐标和轨道根数三种轨道描述形式下的样本进行相关性分析，找出学习特征最优的样本形式，以改善DNN的训练效果；另外，针对摄动兰伯特问题训练样本生成问题，提出了逆向摄动兰伯特问题样本快速生成方法，避免了样本生成过程中摄动兰伯特问题求解。
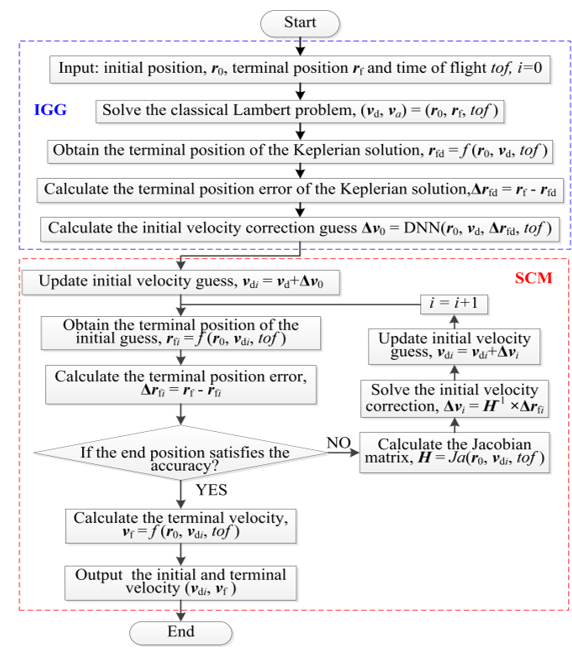
图1 基于DNN的J2摄动兰伯特问题智能求解方法流程图
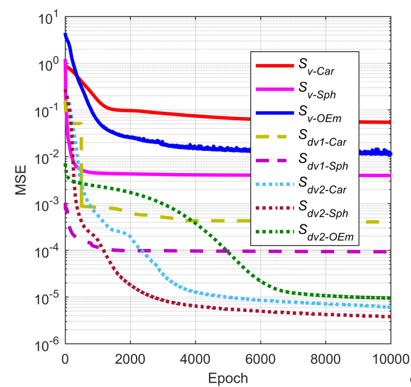
图2 不同形式样本训练结果
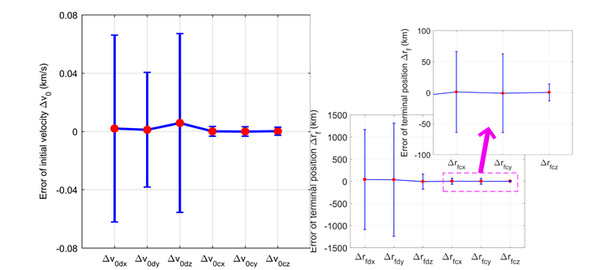
图3 基于DNN的初值生成器预测精度示意图
仿真结果表明所提方法应用于木星 J2 摄动兰伯特问题时，初始速度和终端位置的误差分别限制在 5m/s 和 100km。在10圈内，所提出的方法的计算时间随着圈数的增加以0.047的斜率线性增加，求解10圈摄动兰伯特问题的计算时间小于 0.5 秒。此外，与传统牛顿迭代打靶法以及基于同伦策略改进的打靶算法相比，本文所提方法在确保收敛的前提下，计算效率优势十分明显。因此，本文所提出的基于 DNN 的初值猜测生成策略是一种很有潜力的方法，能够提升打靶算法的收敛鲁棒性并极大地减少打靶算法在解决 J2摄动兰伯特问题的迭代次数和计算成本。
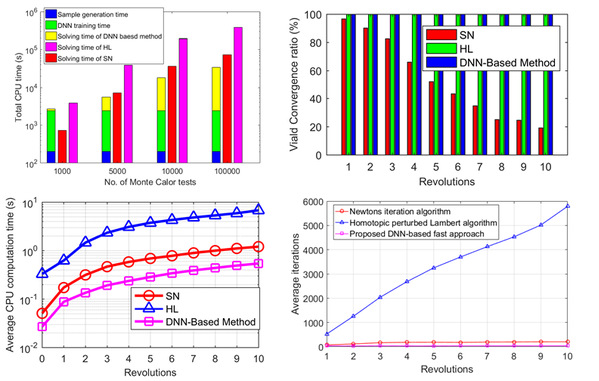
图4 不同方法多圈J2摄动兰伯特问题求解性能对比
该研究工作得到了国家留学基金委、南京航空航天大学博士论文创新与创优基金和空间智能控制技术国防科技重点实验室开放基金的支持，研究成果发表在国际知名航空航天期刊AIAA Journal of Guidance, Control, and Dynamics上。航天新技术实验室博士研究生杨彬为论文的第一作者，李爽教授为论文的通讯作者，南京航空航天大学航天新技术实验室为第一通讯单位。
论文链接：
https://doi.org/10.2514/1.G006091
ResearchGate：
Bin Yang, Shuang Li, Jinglang Feng and Massimiliano Vasile. Fast solver for J2-perturbed Lambert problem using deep neural network, Journal of Guidance, Control, and Dynamics, 2021, DOI：10.2514/1.G006091.
